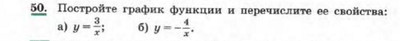Подготовка к контрольной работе по алгебре
№1; №2; №3; №4; №5; №6; №7; №8
Подготовка к контрольной работе по геометрии
№1; №2; №3; №4;
Задания для самоконтроля:
АЛГЕБРА
Тема: "Свойства функций"
(наведите курсор для полного просмотра)
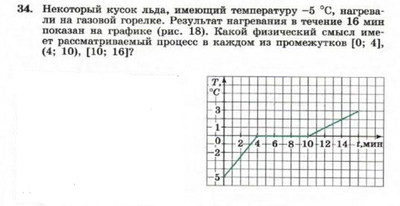
1.
2.
3.
ГЕОМЕТРИЯ
Тема: "Правильный многоугольник"
1.
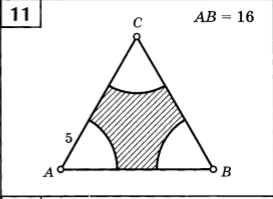
Тема: "Площадь кругового сектора"
1. Найти площадь закрашенной фигуры:
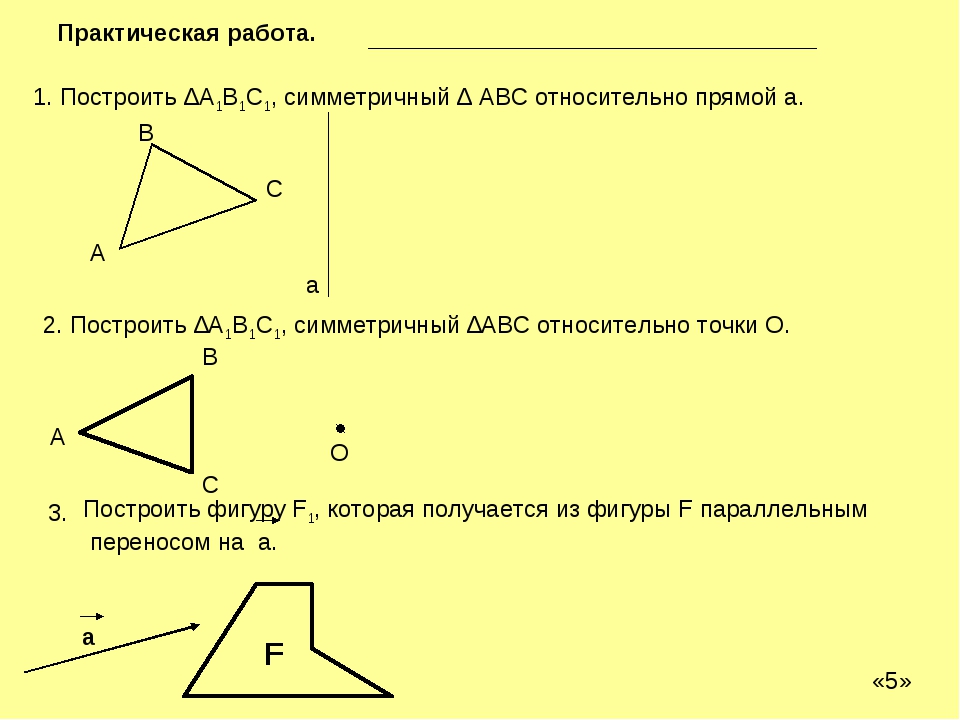
Тема: "Понятие движения"
Выполни задание:
Пошаговое построение сечения параллелепипеда
Построение сечения методом следов – это поэтапное отыскание точек, принадлежащих одной и той же плоскости грани и одновременно плоскости сечения, то есть прямым, проходящим через точки, принадлежащие сечению. Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.
Задача 1. Построить сечение параллелепипеда плоскостью, проходящей через точки
.

Задача 1. Дано
Шаг 1. Чезез точки и
, которые принадлежат одной грани, и, следовательно, одной плоскости, проводим прямую. Точки этой прямой все принадлежат секущей плоскости. Точка
лежит в плоскости основания, поэтому неплохо бы найти найти точку прямой
, которая также принадлежала бы основанию. Для этого проводим прямую
, и находим точку ее пересечения с прямой
–
.

Задача 1. Шаг 1.
Шаг 2. Проводим прямую , принадлежащую плоскости основания. Находим точку пересечения этой прямой ребра
–
.

Задача 1. Шаг 2.
Шаг 3. Точка лежит в задней грани, поэтому надо бы найти точку прямой
, которая принадлежала бы плоскости задней грани. Для этого проведем прямую
, которая принадлежит как плоскости основания, так и плоскости задней грани, и найдем точку ее пересечения с прямой
–
. Через две точки задней грани проводим прямую
, и находим место пересечения этой прямой с ребром
–
.

Задача 1. Шаг 3.
Шаг 4. Окончание построения. Соединяем полученные точки отрезками, и строим многоугольник сечения.

Задача 1. Шаг 4.
Задача 2. Построить сечение параллелепипеда плоскостью, проходящей через точки

Задача 2. Дано.
Шаг 1. Точки и
лежат в одной плоскости, можно соединить их прямой. Прямая
пересечет ребро
в точке
.

Задача 2. Шаг 1.
Шаг 2. Точки и
также лежат в одной плоскости. Соединяем их прямой и отыскиваем точку пересечения ею ребра
–
.

Задача 2. Шаг 2
Шаг 3. Найдем точку секущей плоскости, принадлежащую передней грани, чтобы затем через эту точку и точку можно было бы тоже провести след секущей плоскости. Для того, чтобы найти такую точку, проведем луч
и найдем его пересечение с прямой
– ведь обе эти прямые принадлежат плоскости верхней грани. Точка пересечения – точка
. Точки
и
можно соединить отрезком.

Задача 2. Шаг 3.
Шаг 4. Находим точку пересечения отрезком ребра
– точку
.

Задача 2. Шаг 4
Шаг 5. После этого соединяем отрезками полученные точки и закрашиваем многоугольник сечения.

Задача 2. Шаг 5
Задача 3. Построить сечение параллелепипеда плоскостью, проходящей через точки

Задача 3. Дано.
Шаг 1. Построим прямую , это можно сделать, так как обе точки принадлежат одной грани. Точка
принадлежит грани основания, поэтому нужна точка в этой плоскости.

Задача 3. Шаг 1
Шаг 2. Для того, чтобы найти точку, одновременно принадлежащую и секущей плоскости, и плоскости нижней грани, продолжим прямую и найдем точку ее пересечения с прямой
–
.

Задача 3. Шаг 2.
Шаг 3. Проводим прямую и находим точку пересечения этой прямой с ребром
– точка
.

Задача 3. Шаг 3.
Шаг 4. Теперь надо найти точку в плоскости передней грани, потому что в этой плоскости у нас уже есть точка – точка . Для того, чтобы найти такую точку, продлим прямую
и найдем пересечение этой прямой с прямой
– точка
.

Задача 3. Шаг 4
Шаг 5. Проводим прямую , отыскиваем точки пересечения ею ребер
– точку
, и ребра
– точку
.

Задача 3. Шаг 5.
Шаг 6. Соединяем точки и получаем многоугольник сечения.

Задача 3. Шаг 6
Окончательный вид сечения с другого ракурса:

Окончательный вид
Задача 4. Построить сечение параллелепипеда плоскостью, проходящей через точки
. Точка
в задней грани.

Задача 4. Дано
Шаг 1. Проводим прямую через две точки одной плоскости – и
. Определяем точку пересечения данной прямой ребра
–
.

Задача 4. Шаг 1.
Шаг 2. Продолжение прямой пересечется с продолжением прямой
– так как обе прямые принадлежат плоскости задней грани. Точка
также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка
, и тогда можно провести прямую
.

Задача 4. Шаг 2.
Шаг 3. Точка – точка пересечения прямой
ребра
. Продлим также ребро
и найдем пересечение прямой
и прямой
– точку
, которая принадлежит плоскости основания.

Задача 4. Шаг 3
Шаг 4. Соединяем Точки и
плоскости основания, определяем точку пересечения данной прямой с ребром
– точку
. Соединяем полученные точки отрезками. Штрихуем полученный многоугольник сечения.

Задача 4. Шаг 4.
Окончательный вид сечения с другого ракурса:

Окончание построения